Пре више од 100 година, математичар, рођен у Мађарској, Џорџ Поља нашао се заробљен у кругу друштвене неспретности. Професор на Швајцарском савезном институту за технологију у Цириху, уживао је у усамљеним шетњама кроз шуму ван града. Током једне од ових шетњи, прошао је поред једног од својих ученика и студентове веренице. Онда је, нешто касније, и даље бесциљно лутајући, поново налетео на пар. А касније је то учинио још једном.
Пишући о том искуству у есеју објављеном у књизи из 1970. године, Поља је испричао: „Не сећам се колико пута (ово се десило), али свакако пречесто и осећао сам се посрамљено: изгледало је као да њушкам около, што, уверавам вас, није био случај.
Очајнички желећи да очисти своје име као вребања, Поља је урадио оно што би сваки добар математичар урадио: генерализовао је проблем. Да ли су два луталица математички предодређена да се укрсте? Његова оригинална формулација је поједноставила слику узимајући у обзир само један ходач на бесконачној мрежи. Сваке секунде, шетач насумично бира правац компаса, независно од претходних корака. Полиин математички циљ био је да одреди вероватноћу да ће се шетач на крају вратити на своју почетну тачку. Овај одговор се испоставило да је еквивалентан вероватноћи да ће се два шетача који почну на истој локацији икада поново срести. Открио је да ако шетач заувек лута, они воља вратити на своје почетно место.
О подршци научном новинарству
Ако уживате у овом чланку, размислите о томе да подржите наше награђивано новинарство претплата. Куповином претплате помажете да се обезбеди будућност упечатљивих прича о открићима и идејама које данас обликују наш свет.
Одговор не само да га је ослободио, већ је и открио фундаменталну поделу у томе како закони случајности ступају у интеракцију са физичким простором. Полиини прорачуни су показали да је на дводимензионалној површини (као што је шумско тло), случајном шетачу предодређено да се врати на своју почетну тачку — али у тродимензионалном простору је већа вероватноћа да се та особа никада неће вратити на почетну тачку. Откриће се појављује у хемији и биологији, чак објашњава како одређени молекули ефикасно проналазе одговарајући рецептор на површини ћелија.
Као што је описано у петом издању за 2019 Вероватноћа: теорија и примериаутора Рика Дурета, математичар Шизуо Какутани је досјетљиво дочарао теорему: „Пијан човјек ће на крају пронаћи пут кући, али пијана птица може се заувијек изгубити.“
Овде се „пијана птица“ не односи на зујање мишара, већ на насумични процес на тродимензионалној мрежи (замислите теретану у џунгли). Сваке секунде, птица бира између севера, југа, истока, запада и горе или доле, насумично, независно од претходних избора. Полиа је доказао да ако заувек ходате насумично кроз бесконачно распрострањену градску мрежу, не само да ћете бити загарантовани да се вратите на своје почетно место, већ ћете и погодити сваки место на мрежи бесконачан број пута. Ако, међутим, спроведете исти процес у бескрајној теретани у џунгли, имаћете скоро 66 процената шансе да се никада не вратите на своју почетну тачку. Исто тако два луталице у теретани у џунгли се можда никада неће срести, али два луталица на равној површини морају се срести бесконачан број пута—Полиа није недостајало друштвене милости; недостајала му је трећа димензија у коју би побегао.
Чак и једнодимензионални случај, који се математички понаша као две димензије, има импликације у стварном свету. Замислите да идете у казино са 500 долара у џепу. Табела нуди игру са шансама за победу од 50–50 (боље него што ћете наћи у Монте Карлу). Ако наставите да играте, без обзира коју стратегију клађења користите, на крају ћете пропасти. То је зато што можемо моделирати игру као случајни ход на бројевној правој. Почињете од 500, а након сваке рунде игре крећете се или десно или лево на линији са једнаком шансом. Поља нам каже да, баш као иу дводимензионалном случају, ако играте довољно дуго, неизбежно ћете истражити целу бројевну праву. Ово укључује 0, у ком тренутку ћете банкротирати. Математичари ово зову „пропасти коцкара“, и то објашњава зашто би препоручили да одустанете док сте испред или, још боље, да уопште не играте.
Зашто насумичне шетње нагло мењају карактер између две и три димензије? Иако три димензије природно нуде више простора за лутање од две, само то није довољно као објашњење. На крају крајева, две димензије нуде више простора од једне, али обе показују исто понашање.
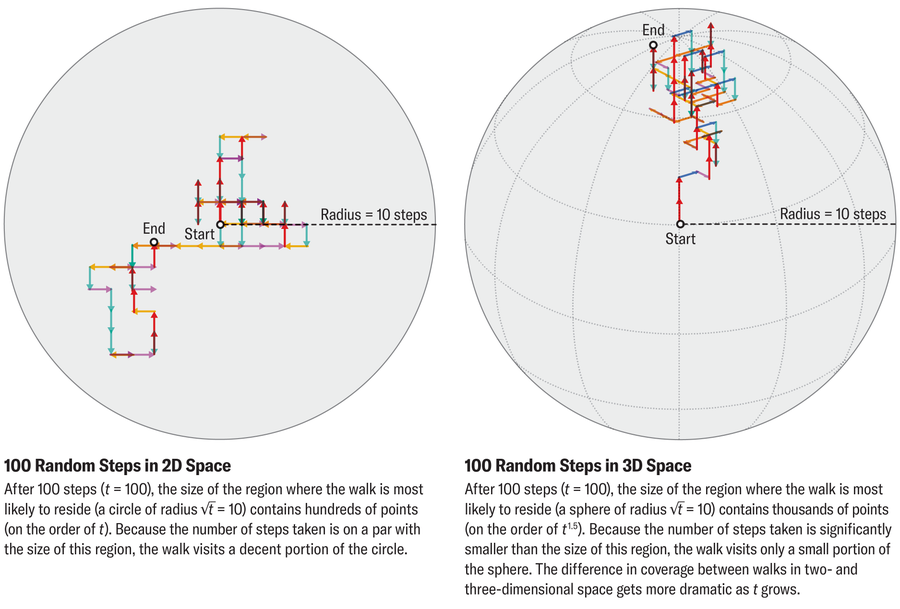
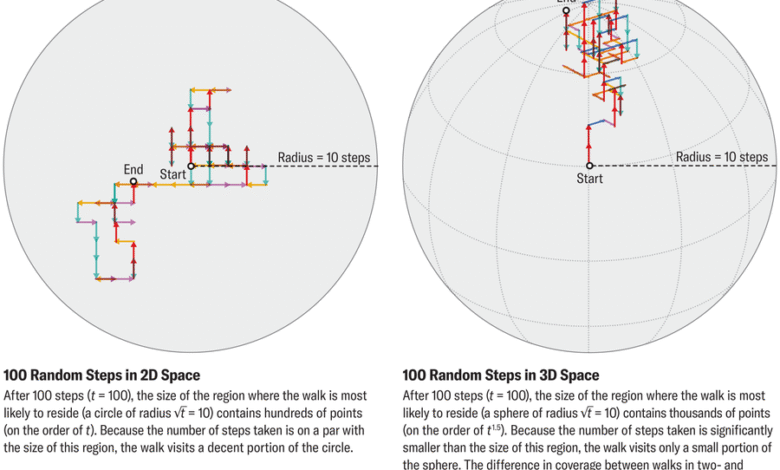
Ако кренете насумично у шетњу за неки коначан број корака које ћемо позвати т, онда обично нећете залутати даље од √т (квадратни корен од т) удаљен од порекла. Конкретно, након 100 корака, већина ходача ће се наћи унутар само 10 корака, или √100, од старта. Интуитивно, насумичне шетње имају тенденцију да лебде у близини исходишта јер се узастопни кораци могу поништити (шетач који направи корак на исток након којег следи корак ка западу уопште није напредовао). Математички, √т једнако је стандардна девијација (статистичка мера распрострањености скупа вредности) удаљености од почетка а т-корак насумично ходање.
Другим речима, ако многи одвојени шетачи почињу на истом месту и лутају независно, онда би графикон њихових растојања од почетка након т корака изгледао као звонаста крива са центром на 0 и са стандардном девијацијом √т. Извођење стандардне девијације за једнодимензионални случај је приступачна вежба ако сте похађали класу статистике — покушајте.
Ово √т фигура важи у свакој димензији и кључ је за разумевање Полиине теореме. Замислите то као радијус региона у којем ће шетач истраживати т степенице. Овај радијус има веома различите импликације у различитим димензијама јер број димензија одређује да ли говоримо о дужини, површини или запремини. Сегмент са полупречником √т има величину реда √т; круг полупречника √т има величину реда т (површина круга је пропорционална полупречнику на квадрат); и сфера полупречника √т има величину по реду т1.5 (запремина сфере је пропорционална полупречнику кубног).
Али без обзира на димензију, шетач који прави т корака не може да посети више од т различите тачке. У једној димензији, број корака премашује величину истраженог региона (т > √т), присиљавајући шетача да се стално враћа својим корацима. У две димензије, број корака одговара величини региона (т = т), омогућавајући шетачу да на крају покрије мрежу, иако танко. Али у три димензије, простор је огроман у поређењу са бројем степеница (т < т1.5), остављајући већину тачака непосећеним и мало је вероватно да ће порекло бити поново посећено.
Наравно, стварни свет ретко личи на савршену мрежу, а птице не бацају новчиће при сваком удару крила. Ипак, овај контраст између дводимензионалних и тродимензионалних шетњи има изненађујуће практичне улоге у природним наукама. Један убедљив пример укључује како хемикалије реагују у нашем телу. Истраживачи често користе насумичне шетње да би моделирали молекуле који се шире кроз другу супстанцу. Замислите да хормон покушава да пронађе одређени рецептор на површини ћелије. Нема механизам за навођење, па се такве реакције дешавају случајним сусретима.
Хормон би могао бесциљно лутати кроз тродимензионалну течност око ћелије све док не налети на своју мету. Уместо тога, многи молекули се лабаво везују за било који прво покажите на ћелијску мембрану. Када се причврсте, клизе по дводимензионалној површини мембране док не погоде циљ. Ово смањење димензионалности претвара спору тродимензионалну шетњу у ефикасну дводимензионалну.
Следећи пут када наиђете на некога кога избегавате, покушајте да тај сусрет претворите у дубок математички увид. Сигурно је боље сакрити се иза дрвета.


