Како је Теен Математичар Ханнах Каиро опоравио главну претпоставку у хармоничној анализи

Када је Ханнах Каиро имала 17 година, опонашала је престанку Мизохата-Такеуцхи, дуготрајно нагађање у области хармоничне анализе о томе како се таласи понашају на закривљеним површинама. Претпоставка је постављена током 1980-их, а математичари су то покушали да докажу од тада. Ако се испоставило да је претпоставка Мизохата-Такеуцхи, то би била истинита, то би на терену осветлила многа друга значајна питања. Али након што је ударио зид након зида, покушавајући то да докаже, Каиро је успео да дође са контра-примером: околност у којој се таласи не понашају како се то предвиђају. Стога претпоставка не може бити тачна.
Каиро је се закачио на проблем након што је доделио једноставнију верзију претпоставке како би се доказао као домаћи задатак за класу коју је преузела на Универзитету у Калифорнији, Беркелеи. „Требало ми је неко време да убедим (курсев инструктор) Руикианг Зханг да је мој предлог заправо био тачан“, каже она. Сада, под Зханг-овим савјетом, она има папир о предприаник сервера Аркив.орг и позвана је да представи своје резултате на међународној конференцији о хармоничној анализи и делимичним диференцијалним једнаџбама у Ел Есцориал-у.

О подржавању научног новинарства
Ако уживате у овом чланку, размислите о подршци нашем награђиваном новинарству Претплата. Куповином претплате помажете да се осигура будућност утицајних прича о открићима и идејама које данас у облику света у облику света.
Каиро каже да воли да прича о својим истраживању и давање презентација са шареним и описним слајдовима (Погледајте примјере у наставку). На питање шта студира, Каиро каже, укратко, „бодове, линије и таласи“.
Рођен и одрастао у Бахамима, Каиро се преселио у Калифорнију са 16 година, где је почела да пређе часове у УЦ Беркелеи. Сад, 18 година, она је на докторима. Програм на Универзитету у Мариланду да настави своје истраживање у теорији фриера рестрикције. Каиро се суочио са многим потешкоћама у њеном путовању, али она је пронашла утјеху и припадала у области математике и на самом раду.
Научни амерички Разговарао је са Каиром о начину на који је хармонична анализа је попут пада камења у још увек рибњак, њен трансродни идентитет и разлоге које воли математику.
(Следи уређени транскрипт интервјуа.)
Иза „бодова, линија и таласа,“ како бисте објаснили своје поље студирања, хармоничке анализе?
Замислите да сте у језерцу, и то је врло још увек рибњак, а ти камен у то. Видите да се ови кружни таласи шире.
Ако баците два камења у језерцу, можда бисте могли приметити овај образац назван умјетни умјет у сметњи: уместо да изгледа као кругове, преклапају се. Добијате велике бодове, ниске тачке. А ти добијате ове занимљиве облике (где се пресијецају). Шта ако бисте користили читаву гомилу таласа – шта бисте онда онда добили? У хармоничној анализи, заправо можете доказати да ако спустите камење на право место у рибњаку, можете добити било који облик који желите.

Клизните из презентације Ханнах Каиро на преношењу Мизохата-Такеуцхи
Моја специјалност је позната као фриерија теорија рестрикције, која је поддисциплина хармоничне анализе у којој радим, где питамо које врсте објеката можемо изградити ако нам је дозвољено само да користимо само одређене врсте таласа. Шта ако нам је дозвољено само да спустимо камење у одређеним деловима језерца? Нећете моћи да добијете ниједан предмет. У ствари, само ћете моћи добити релативно малу породицу објеката. Оно што каже Мизохата-Такеуцхи претпоставка је да је облик објеката који смо добили концентрисани дуж линија.
Шта значи бити „концентрисан дуж линија“?
Један од начина да се помисли на облик објеката је да питате: Шта је закривљење? Постоји неколико различитих начина на који то можете дефинисати. Један могући начин је да се заузме танко, дуги правокутник и питајте колико вашег круга може да лежи у овом танком правоугаонику. Оно што ћете наћи је да то није много тога што може јер се он савија, зар не? С друге стране, ако узмете нешто ставите као ивица квадрата, онда можете добити читаву страну тог квадрата само на једној танкој цеви. Дакле, то значи да квадрат није толико „закривљен“ као круг.
За претпоставку Мизохата-Такеуцхи, кажемо, размотрите овај објекат који градимо из ових таласа. И желимо да кажемо да није баш много лежати на облицима који не садрже веома много линија или танки правоугаонике.
Па како сте успели да оповргнете ову претпоставку?
Погледао сам ове облике и једну ствар коју сам схватио је да су специфична врста таласа који се користе концентрисани дуж дебелих правоугаоника. Ово је заправо нешто што је добро познато. Дакле, на крају гледате ове таласе који су концентрисани на правоугаонике: узимате ове таласе и они се међусобно пресијецају и они чине ове одређене облике, али овде (уместо кружних таласа) користимо правоугаони талас. Дакле, сви су сви ови правоугаони таласи састали једни друге. Оно што сам схватио је да је облик где се састајало није баш под правим углом да се сложи са правцем да су ови правоугаоници указују на то. И то ме је довело до прилично компликоване конструкције користећи фрактале да организују ове правоугаонике.
Оригинална фрактална градња се у ствари не појављује у вашем раду. Који је био твој коначни контра-примјер?
Оно што сам сазнао је да ако организујете ове таласе тако што ћете водити високодимензионалне хиперкубе и пројектовати је у мањи димензионални простор, а затим узети само оне таласе који леже у вашем региону, онда то можете одредити где да их одредите (да их преузмете (да их преузмете).
Шта вас је прво занимало математика?
Одувек ме је занимала математика. Мислим да је за мене математика уметност. У детињству сам био помало усамљен. Математика је била некако тамо као пријатељ. Мислим да уметност не може нужно бити пријатељ на сваком случају да пријатељ може бити, али мислим да је уметност попут пријатеља. И тако, колико год се сећам, одувек сам волео математику.
Реци ми више о томе како вам је математика била пријатељ. Мислим да пуно људи не мисли на математику као веома љубазан.
Постоји аналогија коју волим да направим, што је другом облику уметности: Сликарство. И мислим да ако би неко преузео час на фарбама, могли бисте запамтити датуме и времена на којима су развијени различити облици боје – а можда и које слике су користили које слике су користили. А онда можете схватити који процеси можете да користите да одредите коју врсту боје је. Замишљам да је ово корисно у историји уметности, али ово није уметност …. не бих то требао рећи. Можда је уметност научити о боји. Нећу тврдити да не постоји зато што не учим боју. Али мислим да је математика помало таква таква у школи, људи уче о (математичкој верзији) боје; Не уче о сликарству.
Математика ми је утешно јер је начин истраживања и истраживања идеја и размишљати о њима и да изградимо више идеја из других идеја. Оно што је утешно због тога је то независно од света на неки начин. Ако имам тужан дан, срећан дан, ако се преселим у Мариланду (управо сам се преселио у Мариланду), математика је и даље ту и још увек је иста ствар. То је такође нешто што ми мозе да заузме ума.
Поменули сте ми да сте трансродне. Како је то утицало на ваше путовање?
Мислим да је то вероватно релевантније на моје путовање као особа него као математичар. Бити транс ме је присилио да видим ствари о свету да можда иначе не би видео. Натјерао ме је да видим свет другачије и натерао ме да људи другачије видим и натерали ме да се другачије видим.
Срећом, у математичкој заједници, мислим да је већина математичара у реду са транс људима. Мислим да је некада било значајније (у мом дану дана) него што је то сада. Ових дана то заиста не чини велику разлику.
Зашто сте одлучили да сада идите на записник као транс?
Транс видљивост је важна. Људи имају идеје о томе ко су Транс људи, и мислим да је најбоље проширити то. Можда се такође надам да људи који мисле да су трансгене „мање“ него што би људи ЦИСГЕНДЕР-а могли да то испитају то.
Друга ствар је да је добро за Транс људи да знају да нису сами. Мислим да тај део онога што помаже транс-ама који схвате да су транс да знају да постоји више опција за кога можете бити као транс личност. То ми је важно.
Хвала вам пуно што сте то делили. Где је ваше омиљено место за математику?
Ако покушавам да будем продуктиван у писању нечега, онда волим да будем за столом и волим да слушам Бацх. Ако само покушавам да размислим о идејама, онда је моје омиљено место да то учиним негде где не морам да обраћам пажњу на веома друго друго. Могао бих само да седим негде размишљајући о стварима или бих могао да прошетам напољу.
Такође волим да разговарам са другим људима о математици, што је још једна врста математике. Стварно волим да дам презентације о математици. Имам ове рукописне клизне клизне са свим тим бојама и цртежима. Срећом, у хармоничној анализи, могу да дам овако презентацију, а онда су сви тако срећни и они ми кажу да су ми слатки слаткиши.
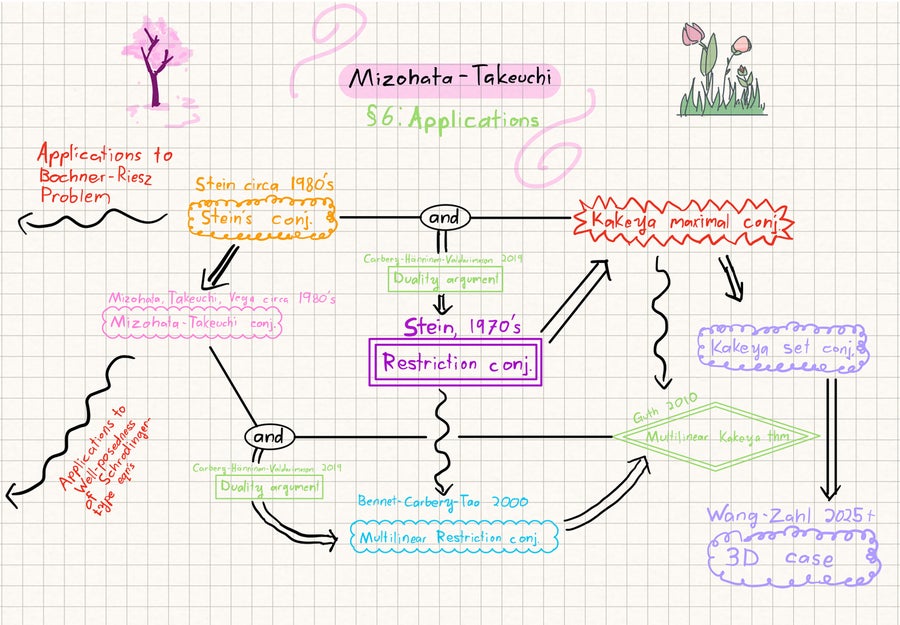
Завршни клизач из Каирове презентације на преношењу Мизохата-Такеуцхи
Шта је следеће за ваше истраживање?
Радим на истраживачком пројекту са својим саветником о Мизохата-Такеуцхи и суседним стварима и о неколијој различитој ствари: локални Мизохата-Такеуцхи претпоставка.
Процес учења више о овој врсти математике прилично је узбудљиво – не само да ме више учим више о ономе што је вани, али за математичку заједницу у целини да покуша да боље схвати ове врсте ствари боље. (То је нешто због чега сам узбуђен.



