Студенти проналазе скривене ФИБОНАЦЦИ секвенце у класичној слагалици вероватноћи

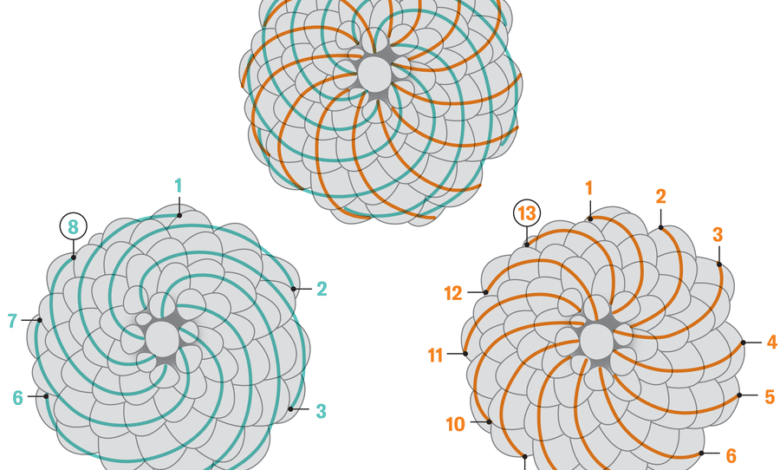
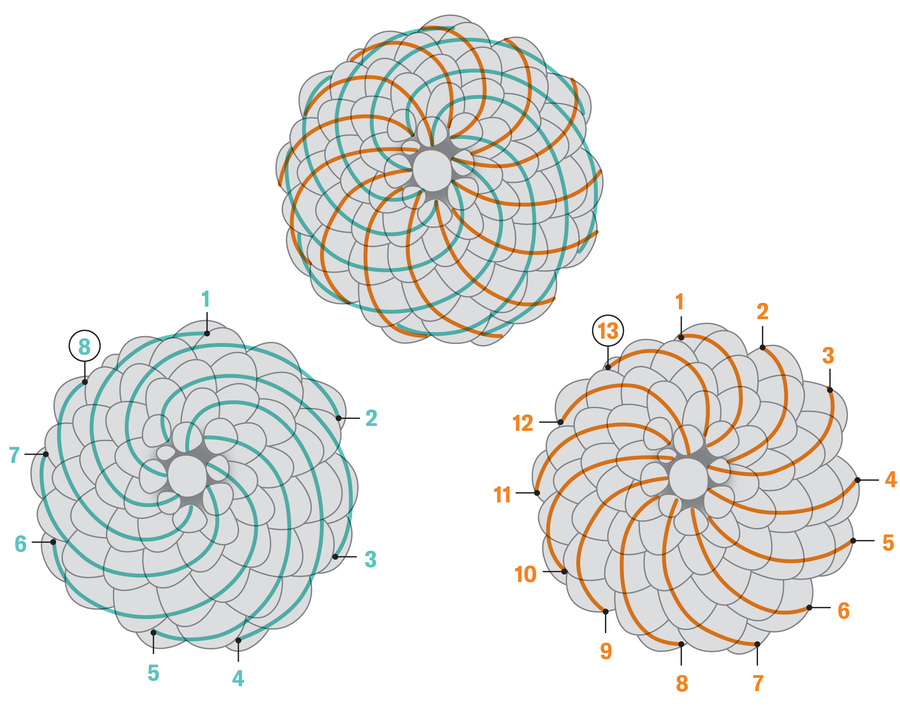
Варијација слагалице под називом „Пицк-уп палице Проблем“ поставља следеће питање: ако имам неки број штапова са случајним дужинама између 0 и 1, које су шансе да не могу да формирају троугао? Испада да је одговор на овај квандар има неочекивани паралелан са обрасцем који је пронађен по природи.

ФИБОНАЦЦИ секвенца је наручена збирка бројева у којима је сваки термин једнак претходној два додате заједно. Овако иде: 1, 1, 2, 3, 5, 8, 13, … и тако даље. Ови се бројеви приказују практично свуда. Ако погледате биљку са спиралима, попут боровог конуса или ананаса, вероватније него не, број спирала који иде у сваком правцу биће узастопни услови ФИБОНАЦИ секвенце. Али пар младих истраживача био је изненађен што је открио да су овај образац и проблем за палице за преузимање дубоко повезани.

О подржавању научног новинарства

Ако уживате у овом чланку, размислите о подршци нашем награђиваном новинарству Претплата. Куповином претплате помажете да се осигура будућност утицајних прича о открићима и идејама које данас у облику света у облику света.

Проблем са палицама за преузимање је варијанта „Пропуштеног палице“, који се може пратити на најмање 1854. У својој најједноставнијој итеративној проблемима, проблем са прекидачем затражи вероватноћу да се палица поквари насумично у три комада може да формира троугао. (У проблему са преузимањем, дужине не морају да се садрже одређене целине, тако да се могуће дужине различито дистрибуирају.) Више од једног века касније, у Октобар 1959. године од Научни Американац, Мартин Гарднер је написао о проблему сломљеног штапа За његове математичке колоне игре. Гарднер је то истакао као класичан пример контраинтуитивне природе проблема у вероватноћи и статистике. У препринт папир Објављено на сервер аркив.орг у мају, млади истраживачи и њихови сарадници истражују нову варијацију проблема са прикупљањем преузимања.

Овај напор је започео када је Артхур Сун, првогодишњи додипломски студент на Универзитету у Цамбридгеу, осмислио је проблем за конкурс за математику универзитета. Каква је вероватноћа, питала се да је од четири штапа са случајним дужинама између 0 и 1, ни три, није могла да направи троугао? Уписао је помоћ свог пријатеља Едварда Ванг-а, у то време 12. разреда у Сцотцх Цоллегеу, средњој школи у Аустралији, где су се и сунце првобитно упознали. Заједно, Ванг и Сунце су постељили проблем на својим рачунарима и трчали насумична суђења и изнова, пратећи резултате сваког суђења. Чинило се да је пар да четири штапа не могу да направе троугао међу њима врло близу једног од шест дана.

Убрзо су Ванг и Сун почели да се питају шта је одговор био за веће групе штапова. Они су уписали помоћ Давида Треебија, математичар који је повезан са АУСТРАВИЈОМ УНИВЕРЗИТЕТОМ и учитељем у Сцотцх Цоллегеу. Група је трчала још више симулација, а ускоро је почео да се појављује узорак.

Према симулацијама истраживача, ако н Да ли је број насумично одабраних штапова, шанса да не има важећи троугао међу њима био је реципрочна прва н ФИБОНАЦИ БРОЈЕВИ МНОГОЛИКИЈИВИ. На пример, ако насумично изаберете шест штапова, вероватноћа да не можете да направите троугао са њима је 1 / (1 × 1 × 2 × 3 × 5 × 8) = ¹/₂₄₀. Тим је био изненађен што је познати редослед повезан са проблемом троугла. „Не бисмо имали разлога да сумњамо да би то било,“ Трееби каже: „Али то је било немогуће да није било.“

Истраживачи су почели да развијају доказ зашто ова веза мора бити тачна, али им је требала стручњак за статистику да га све повуче заједно. Донели су четврти сарадник, бившег морасх математичара Аидан Судбури. Сретно је уживао у пензији када му је тим пришао.

„Одмах сам је ударио какав је био шармантан проблем“, каже он. „Дивно!“ Заједно, четири истраживача су изразила чврст доказ обрасца који су сунце и Ванг приметили. Иако Сродни резултати су доказани коришћењем сличних метода и обухватају широк спектар проблема и троугаоних проблема, неки стручњаци на терену сматрају да је све једноставно освежавајуће у реду. „Шта је лепо у томе је: Врло је добро написано“, каже Стевен Миллер, математичар на Виллиамс Цоллегеу и председнику ФИБОНАЦЦИ удружења. „То је доступно, лако је читати и продужава врло познати проблем.“

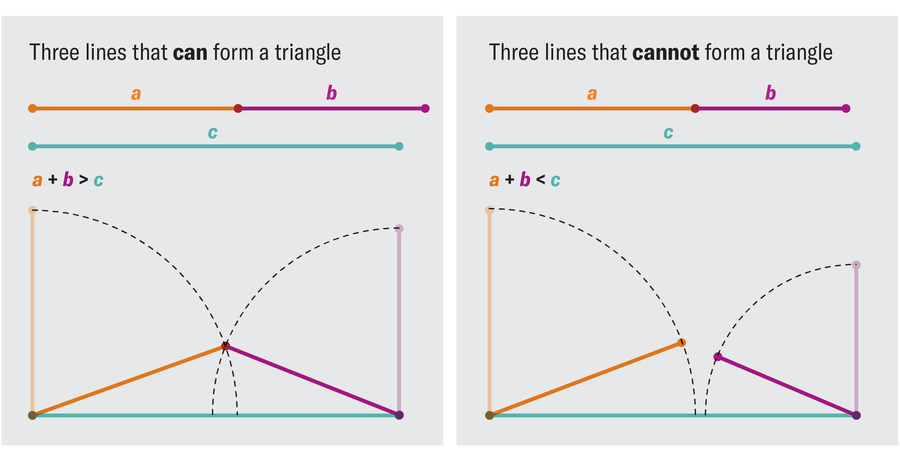
Да бисте разумели решење за палице за преузимање, размислите о најмањим могућим случају. Претпоставимо да имате три палице са насумичним величинама између 0 и 1. било које три штапића могу да формирају троугао ако, и само ако, ниједан палица није дужа од осталих два састављена. Ако имате палице дужине 1, 2 и 300, без обзира на то колико је угао који сте ставили између њих, прва два штапа се никада није могла довољно протезати довољно широм да се треће прилагоди трећини. То се назива „неједнакост троугла“: ако а, б и ц представљају дужину штапова од најглупље до најдуже, они ће једноставно формирати троугао када а + б ≤ ц.

Пронаћи вероватноћу да три случајне дужине формирају троугао, математичари могу размотрити сваки сет од три дужине као тачку у тродимензионалном простору (на пример, дужине) ¹/₂, ¹/₆ и ¹/₃ представљају тачку (¹/₂, ¹/₆,¹/₃)). Пошто дужина падају између 0 и 1, скуп свих таквих тачака може представљати јединичну коцку:

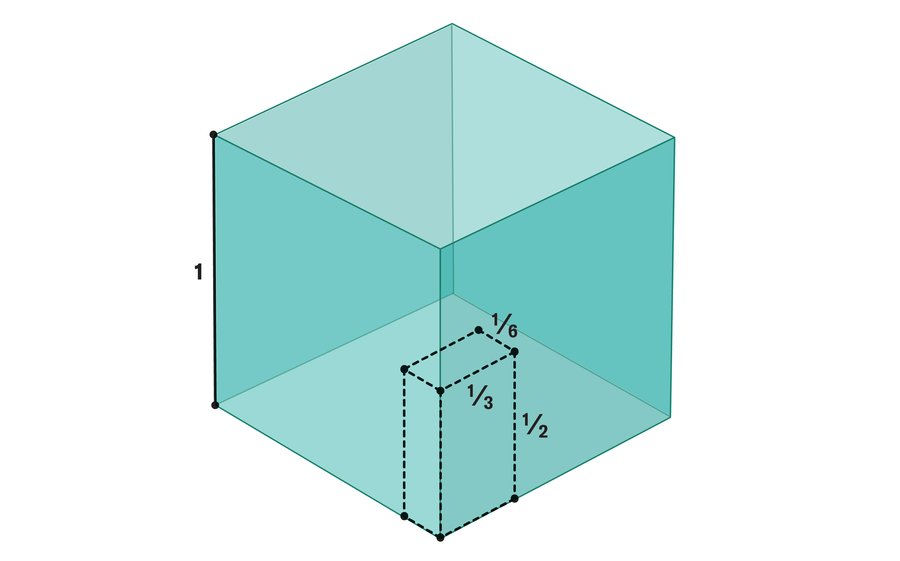
Истраживачи тада погледају подскуп ове коцке у којој бодови задовољавају троугла неједнакост – облик који изгледа овако:

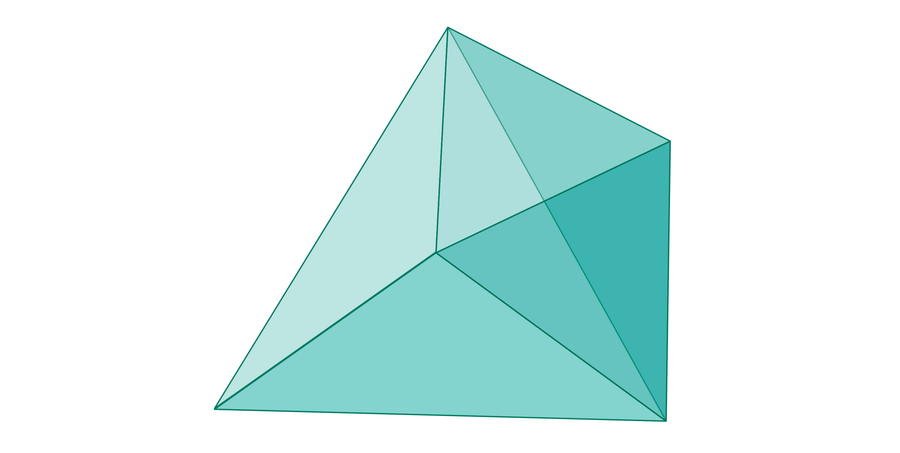
Са мало геометрије испада да је овај облик тачно половина количине коцке. Стога ће три насумично одабране дужине моћи да формирају троуглу тачно половину времена, као 1 / (1 × 1 × 2) = ¹/₂.

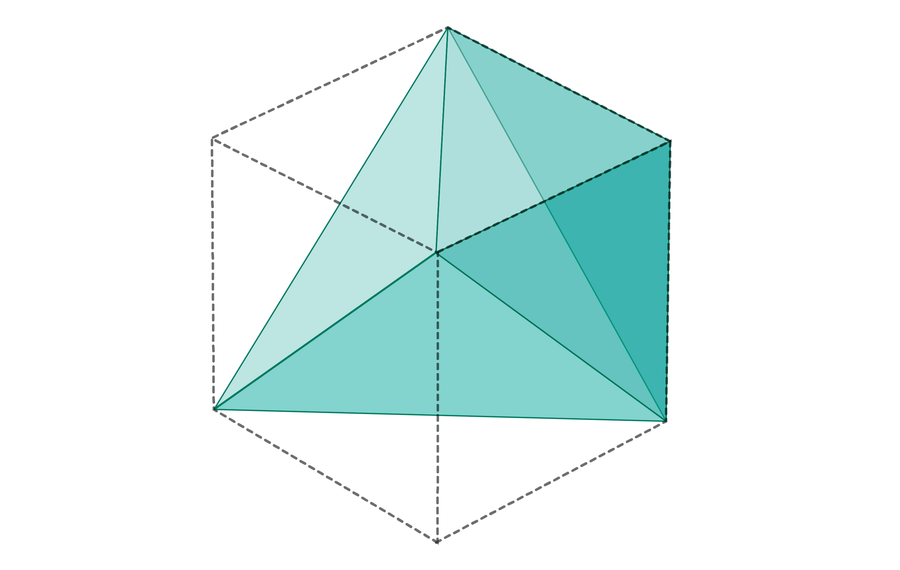
Где улази Фибонацције? Претпоставимо да је прикупљање било којег броја штапова наложено од најглупље до најдуже. Ако није три међу њима да формирају троугао, свака дужина штапа мора бити већа или једнака збиру претходне две – у супротном, та три штапа могу да направе троугао. У ФИБОНАЦИ секвенци, сваки број је прецизно једнак збиру претходне две. Другим речима, сваки сегмент ФИБОНАЦИ секвенце је што је могуће ближе да се троугао у њему не заправо нема. У треебиним речима, „ако ми похлепно избјегавамо троуглове), фибонаццијев секвенца се природно појављује.“

Истраживачи сматрају да би требало да постоји неки пут директно из овог увида на доказ о прикључком за прикључци за преузимање теорема. Међутим, они то нису могли пронаћи. „Надали смо се да ћемо пронаћи нешто што је било мало више … интуитивно, али нисмо могли да формализујемо наше мишљење“, каже Трееби. Уместо тога, њихов рад користи интегралне интеграле да би се израчунали високодимензионалне количине директно-метода мало попут гледања на подручје унутар коцка изнад (али без визуелне референце). Истраживачи тренутно нису на путу за другачији доказ – али надају се да ће неко други наћи један.

Време је да устанете за науку

Пре него што затворите страницу, морамо да тражимо вашу подршку. Научни амерички Служио је као заговорник за науку и индустрију током 180 година, а тренутно мислимо да је тренутно најкритичнији тренутак у историји двоструке века.

Не тражимо добротворну организацију. Ако ти Постаните дигитални, штампани или неограничени претплатник На научноамеричке Америке, можете да осигурате да је наша покривеност усредсређена на смислено истраживање и откриће; да имамо ресурсе за извештавање о одлукама које прете лабораторију широм САД-а; И да подржавамо и будуће и радне научнике у то време када вредност саме науке често не буде непризната. Кликните овде да бисте се претплатили.