Проблем са слагањем математике има глупог раствора

Овај блок за слагање математичког проблема има надолазеће решење које требате да верујете да верујете
У принципу, ова немогућа математика омогућава мост без лепљења слаганих блокова који се могу протезати преко Гранд Цанион-и у бесконачност
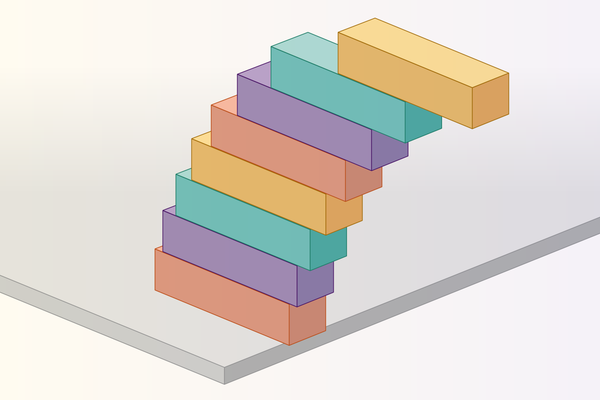
Ево експеримента у размаку ума који можете испробати код куће: окупите неке дечије блокове и ставите их на сто. Узмите један блок и полако га гурните преко ивице стола, инча за инчу, све док не буде на ивици пада. Ако поседујете стрпљење и сталну руку, требало би да га уравнотежите тако да тачно половина виси са ивице. Гурнути га даље, а гравитација побеђује. Сада узмите два блока и почните испочетка. Постављате један на крај другог, колико далеко можете добити крај горњег блока да бисте покуцали на ивицу стола?
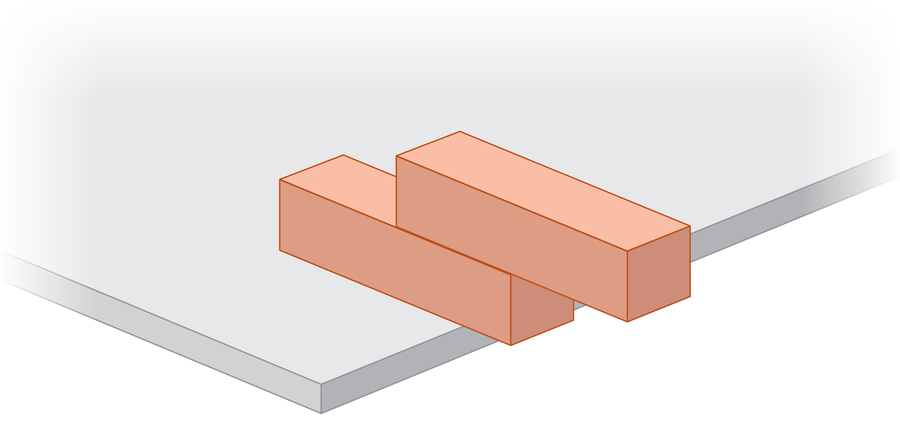
Наставите даље. Слањање што више блокова, који је најудаљенији прекривач који можете постићи пре целог конструкције? Да ли је могуће да торањ продужи дужину целог блока изван усне стола? Да ли физика дозвољава два дужина блока? Запањујући одговор је да се слаг мост може заувек разнијети. У принципу, слободни хрп блокова може да обухвати Гранд Цанион, није потребно лепљење.
О подржавању научног новинарства
Ако уживате у овом чланку, размислите о подршци нашем награђиваном новинарству Претплата. Куповином претплате помажете да се осигура будућност утицајних прича о открићима и идејама које данас у облику света у облику света.
Не кликните „ЦХАЛТОУТ“ само на бесконачном паковању Јенга блокова још увек. Практичности у стварном свету као што су неправилни блок облици, ваздушне струје и дробљење бескрајне грађевине могу отежавати ваше инжењерске тежње. Ипак, разумевање зашто прекривач нема ограничење у идеалном математичком свету је просветљујуће. Објашњење шарке на математичким хармоничним серијама и концепту физике центра масе, две наизглед једноставне идеје са напајањем. (За више забаве, погледајте: Колико високи можете изградити куле без да се то превлада?)
Ваша интуиција би вам могла рећи да један блок може објесити пола њене масе изван ивице стола пре превисања. Али зашто је то тако? Сваки објект има средиште масе – једна тачка на којој можемо замислити да је тежина целог објекта концентрисана када размишљамо о равнотежи. Све док центар масе седи изнад стола, објект остаје да се стави. Међутим, у тренутку када центар масе прође преко ивице, међутим, гравитација ће повући целу ствар. У случају кашике, предмет са неправилном дистрибуцијом тежине, можемо да објесимо више од половине дршке посуђа на ивици пре него што је савета, јер је средиште масе ближи глави, где више од пребивалишта тежине. За наш сложени мост претпостављамо да су наши блокови идентични, са јединственом густином (то јест, у неким деловима не, они нису гушћи у неким деловима од осталих), тако да сваки нечији центар масе седи на средњој тачки.
Када додамо још блокова, морамо да објаснимо средиште масе целог куле. Размотрите случај два блока. Знамо да горњи блок може продужити половину своје масе изван оне испод ње. Али након тога, колико далеко можемо да потиснемо доњи блок?
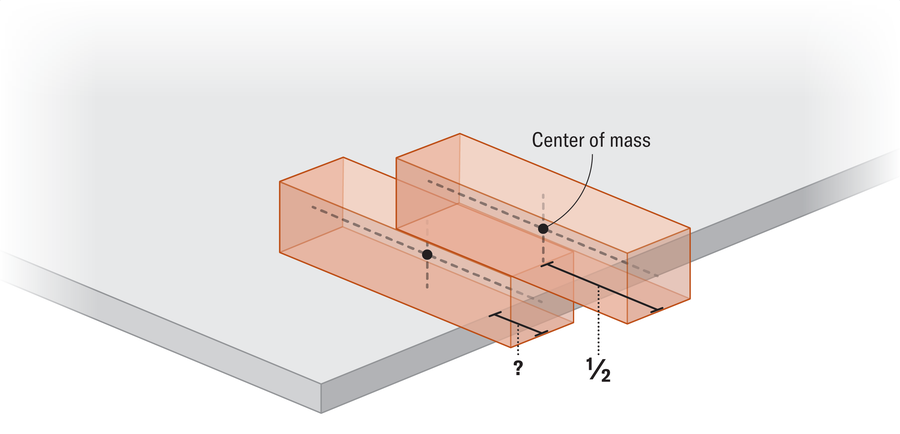
За једноставност, рецимо да сваки блок има дужину од 1 и масу 1. Доњи блок можете да избаците само четвртину пута (у поређењу са пола њене дужине преко ивице када је то било сама). У том тренутку, центар масе горњег блока и средиште масе доњег блока једнако је са ивице стола (центар масе горњи блок седи четвртину десно од ивице, а средиште масе доњег блока, а лево од ивице). Тако у комбинацији центар масе систем два блока почива савршено избалансирана изнад ивице стола.
Образац се појављује док настављамо да додајемо блокове структури. Горњи блок се протеже 1/2 Иза ње, други блок се протеже 1/4 изван блока испод ње, трећи се протеже 1/6четврти се протеже 1/8а затим се накнадни блокови продужавају 1/10, 1/12и тако даље. Да погледамо зашто, погледајмо још један пример. Претпоставимо да имамо стабилни торањ који садржи пет блокова, а желимо да додамо шести блок испод њега, а затим клизните целу структуру колико можемо. Помоћно је концептуализовати ову слику као само два блока: један са масом од 5 врхова једним блоком масе 1. Прво ћемо да прерадимо тешки блок колико ће то ићи тако да његов центар масе седи на ивицу доњег блока. Тада можемо тачно да гурнемо доњи блок 1/12 од јединице изван ивице стола. Како то знамо?
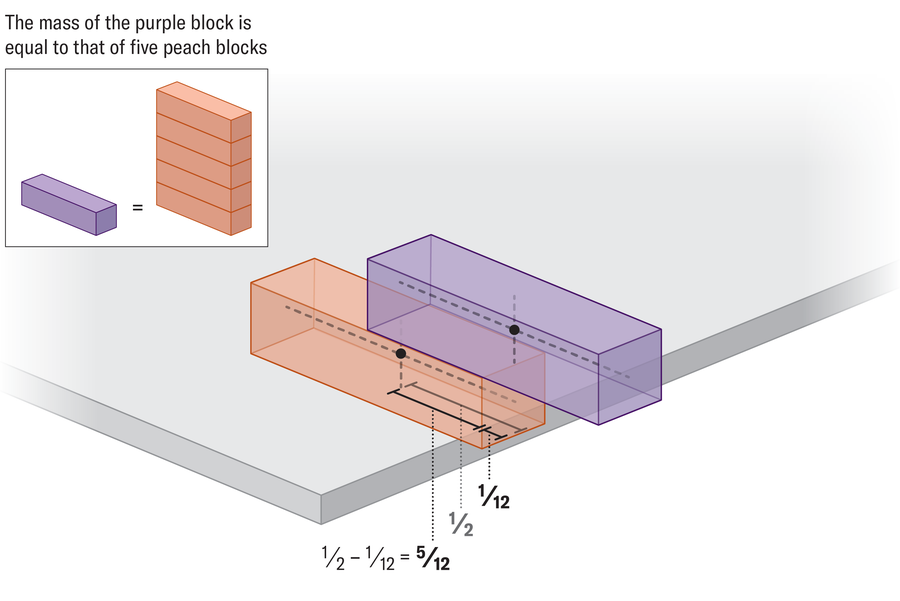
Опет, одговор се спушта да уравнотежи центре масе два блока, само овог пута, јер је доњи блок пет пута упаљач, његов центар масе мора завршити пет пута даље на таблици на тежини тежине тежих блока. Ово је познато као закон полуге – размишљати о томе како се књига осећа теже на вашем длану, дакле, померите га од свог тела, тако да би меке корице у потпуној продуженој руци могао осећати еквивалентно у уџбенику која се налази близу вашег ТЕРСО-а. Удаљеност између центра масе горњег блока и ивица стола је 1/12а удаљеност за доњи блок је 1/2 – 1/12 = 5/12или пет пута више. Сличан израчун открива исправан преношење на свим нивоима куле.
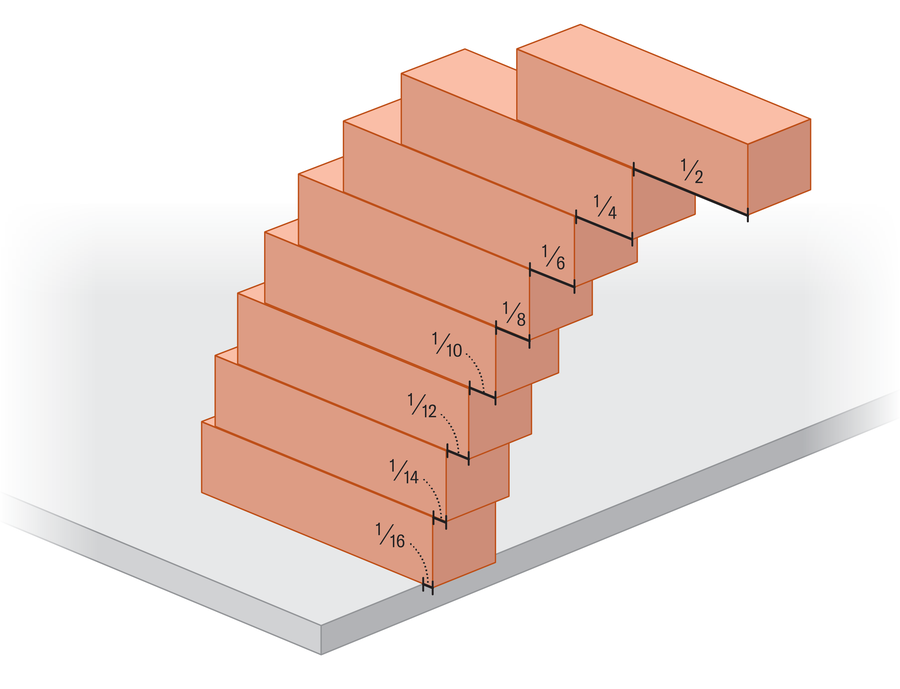
Одговарање на наше уводно питање (колико далеко може продужити кули?) Износи све ове узастопне преношења. Ако имате 10 блокова, могу се продужити на 1/2 + 1/4 + 1/6 + 1/8 + 1/10 + 1/12 + 1/14 + 1/16 + 1/18 + 1/20што додаје до око 1.464 дужине блока изван ивице. Али шта је граница колико далеко можемо да ставимо блокове? За то морамо додати бескрајно много од ових смањујућих услова. Добијени узорак сноси упечатљиву сличност на једну од најпознатијих бесконачних сума у математици, хармоничној серији, која узима узајамни број сваког бројања (који је, 1 подељен са сваким позитивним целим бројем) и све их све позитивно налазе:
1 + 1/2 + 1/3 + 1/4 + 1/5 + … и тако заувек.
Ако пажљиво погледате, можда ћете приметити да су прекривачи из проблема са слагањем блока тачно половина сваког од ових услова: 1/2 + 1/4 + 1/6 + 1/8 + 1/10 + …
Калкулус, грана математике која копа у томе како нас ствари мењају, подучава нас да чак и када додате бесконачно много смањујућих израза, понекад се сума контрарише на коначну вредност и понекад се разликује у бесконачности. Укупно хармоничке серије расте невероватно полако. Првих 100.000 појмова додају око 12.1, док први милион појма једнак само око 14.4. Ипак, на немилосрдном пужевом темпу, хармонична серија расте заувек.
Сваки појединачни прекривач у проблему слагања блока једнака је половини мандата у хармоничкој серији. Јер је половина бесконачности још увек бесконачност, торањски потенцијални превелици такође нема везан.
Наравно, превођење чисте математике у пракси увек долази са препрекама, али проблем са слагањем блока нуди забавни изазов за спречавање. Са само четири блока требало би да будете могли да продужите горњу дужину пуне блокове поред ивице (1/2 + 1/4 + 1/6 + 1/8 = ~ 1.042). Да бих испунио моју новинарску душну марљивост, пробао сам ово код куће са играњем карата на столу за кафу. Након неколико минута пацијента, успео сам да уравнотежим горњу картицу одмах изван ивице, а са њим сам се у потпуности дружио са столом и осећао се као мађионичар.
Две дужине пуних блокова изван било које површине захтевало би 31 комада. У међувремену од 100 милиона дијелова не би вам било чак и пуне дужине преноса 10 блокова, јер сума првих 100 милиона услова у хармоничкој серији све је подељена са 2 једнака око 9.5. Дакле, требаће мало гриц да се обухвати велики кањон. На огромним вагама физика почиње да се сруши забаву математичара. Али у идеализованим условима где је средиште масе и само складна серија владају, могућности су буквално бескрајне.




