Како је грешка у култној класичној игри Доом изазвала ново признање за Пи
Сви праве грешке — а понекад те грешке могу довести до изненађујућих открића. Почетком 1990-их, док је програмирао компјутерску игру Доом, програмер игара Џон Кармак је ручно поставио вредност пи (π) — и на прави штреберски начин, записао је број на девето децимално место из меморије: 3,141592657.
Примећујете ли нешто чудно на тој фигури? Последња цифра је погрешна. Уместо тога, број би требало да буде 3,141592654. (Пи се често скраћује без заокруживања, у ком случају би девето децимално место било попуњено са 3, али се заокружује на 4 јер је следећа цифра 5.)
На срећу, ова грешка има мало утицаја на игру. У Доому, једном од најранијих пуцачина из првог лица са тродимензионалном графиком, преузимате улогу свемирског маринца који због неуспелог експеримента телепортације завршава на месецу Марса, где се бори против демона и зомбија. Игра има сјајну причу, али ужасну графику. То није због погрешне вредности пи, већ због тога колико је мало рачунарске снаге било доступно 1990-их.
О подршци научном новинарству
Ако уживате у овом чланку, размислите о томе да подржите наше награђивано новинарство претплата. Куповином претплате помажете да се обезбеди будућност упечатљивих прича о открићима и идејама које данас обликују наш свет.
Ипак, грешка је инспирисала америчког инжењера Лукеа Готслинга да истражи могуће последице погрешног програмирања пи у већој мери у игри – идеја коју је изнео на хакерској конференцији 2022.
Када Пи није у праву у компјутерској игрици
Пошто је Доом компјутерска игра отвореног кода, можете преузети код—и модификовати га. Готслинг је управо то урадио, тестирајући шта би се десило ако би променио програмиране вредности пи.
Резултати могу учинити да се гледалац осећа помало мучно. Када је Готсзлинг поставио π = 3, на пример, пикселизовани свет Доома постао је изобличен, а зидови и стубови су се померали на неочекиване начине. Ипак, игра се могла играти.
Када је пи постављен на вредност Ојлеровог броја, 2,718…, чудност се појачала. Како се играч кретао право у свету игре, околни објекти би се померали на различите стране. Непријатељи су се могли појавити ниоткуда и поново нестати. „Са довољно опијености, ово можете поново да креирате“, нашалио се Готслинг у својој презентацији.
Ствари су постале јако лоше када је поставио вредност π⁄2 за пи. Зидови би блистали и нестајали. Невидљиве препреке блокирају кретање играча. Игра није била посебно забавна у овом стању.
Пи није увек 3.14159…
Зашто је пи тако моћан? Да бисмо одговорили на то, морамо дубље размислити о последицама промене пи.
Првобитно, пи је дефинисан као однос обима круга и његовог пречника. У нашем свакодневном свету претпостављамо да су кругови округли. Али у ужем математичком смислу, круг је дефинисан свим тачкама које су једнако удаљене од заједничког центра. У равном, дводимензионалном свету, где су удаљености дефинисане као најкраће праве линије, круг је округао. То значи да се вредност пи може променити.
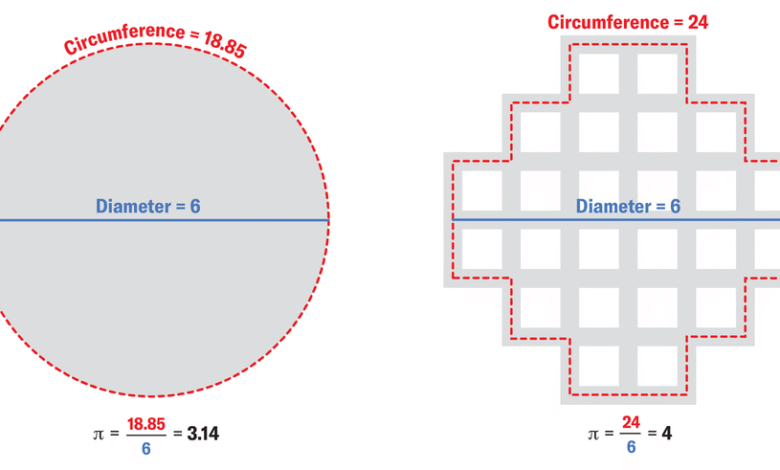
На пример, замислите да стојите у центру Менхетна. Ако желите да сазнате која су места тачно један километар од вас, облик који можете да креирате више неће бити округао. То је зато што не можете да прођете кроз зидове. Уместо тога, морате да пратите распоред улица. Круг има квадратни облик у „Мехетнској метрици“, како се зове у математичком жаргону. А ако дефинишете пи у овом контексту као однос обима и пречника, број поприма потпуно различите вредности: у метрици Менхетна, пи је тачно 4.
Ако боље погледате, вредност пи у нашем свету није баш 3,14159…. Уместо тога, однос обима и пречника добија другачију вредност – и, што је још горе, ова вредност варира!
На пример, ако стојите на Северном полу и посматрате сва места тачно 1000 километара удаљена од вас, ове тачке формирају круг на површини сфере — али је њен обим мањи од обима круга на равној површини, захваљујући закривљености Земље. Што се приближавате екватору, тај ефекат постаје јачи, а одговарајућа вредност пи све више одступа од уобичајених 3,14159….
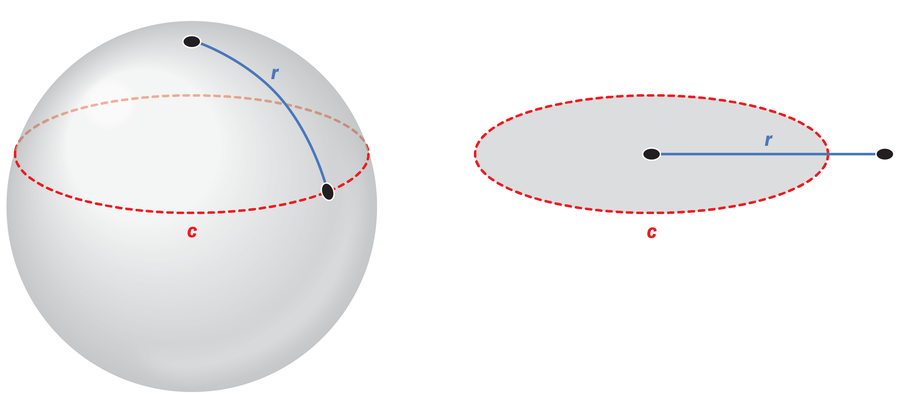
Нова вредност пи стога није константна, већ зависи од полупречника круга. И то није само случај када се разматра сферна површина. Било која врста закривљене површине даје променљиве вредности за пи.
Математичари такве закривљене светове називају „нееуклидском“ геометријом. (Пре више од 2000 година, научник Еуклид је изложио правила геометрије која је већина нас научила у школи — идеје које се примењују само на равном свету.)
Креирање Триппи Висион оф Доом
Необичан пејзаж Готсзлинга који је створио подешавањем Доомовог изворног кода је нешто сасвим друго. Да бисмо то разумели, морамо да се вратимо у деведесете: време када је свака аритметичка операција трошила огромну количину ресурса. Да би решили тај изазов, програмери су уложили напоре да унапред одреде могуће прорачуне и сачувају их у „табелама тражења“.
Приликом развоја 3Д графике за компјутерску игру, тригонометријске функције као што су синус, косинус и тангента играју важну улогу. Могу се користити за описивање како се објекти крећу кроз простор током времена. Да би уштедели процесорску снагу, Доом-ови програмери су унапред израчунали важне вредности тригонометријских функција за различите углове и ускладиштили их у табелама тражења. И овде долази до пи: морате да помножите угао у степенима са пи да бисте добили одговарајућу вредност у радијанима, коју рачунар користи.
Дакле, ако би Готслинг користио вредност пи која је била премала, углови би били погрешно конвертовани. Пошто програмери чувају само коначан број углова, он је направио табеле за тражење са вредностима које више не укључују пуне ротације: уместо да опише окружење у коме се објекат поново појављује на истом месту након ротације од 360 степени, ово се дешава након знатно мањег угла. Као резултат тога, у екстремним ситуацијама, објекти изненада нестају или се поново појављују ниоткуда.
Доом свет који је Готслинг створио је невероватно чудан. Ипак, то је леп начин да наведете људе да размишљају о математици и вредности — у сваком смислу — броја пи. Једна мала грешка програмера игре изазвала је много већи експеримент са чудним бројем круга.
Овај чланак се првобитно појавио у Спектрум дер Виссенсцхафт и репродуковано је уз дозволу.




