Испробајте ове логичке загонетке са међународне логичке олимпијаде

Колико сте логични? Испитајте своје вештине овим проблемима са нове међународне логичке олимпијаде
У само другој години, међународна логичка олимпијада већ процвата јер је логика постала све кључнија у нашем свету који се мења

Раније овог месеца, 36 оштрих средњошколаца из околих света пролазило је стопало на топлом и брачном кампусу Универзитета Станфорд. Од више од 4.000 ученика из више од 2.000 школа у више од 90 различитих земаља, ове 36 људи је одабрано да се такмиче као финалисти на другом икада међународној логичкој олимпијади (ИЛО).
Конкуренција је обухватила три рунде тестова, кулминирајући у финалу на Станфорду. There teams of two to four engaged in a battle of wits, solving logic puzzles and competing in mathematical games against the backdrop of the foothills of Palo Alto, Calif. The winners this year were 11th-grade students Luke Song, Zixuan Yin, Kingston Zhang and Max Yang, who, unhappy with their official moniker of “Team I,” informally dubbed themselves “Team Goblin Tribe” after a video Скит који су гледали током сесије прегледа. Кључ њиховог успеха, тврде се, било је пуно праксе и тимског рада. „Мислим да смо дио разлога зашто смо то могли да учинимо добро у томе, јер знам своје саиграче заиста добро и били смо пријатељи већ много година“, каже песма.
ИЛО је лансирао Станфорд Цомпутер Сциентист и логичар Мицхаел Гесеретх у сарадњи између универзитета и образовне непрофитне лумине. „Користимо логику у готово свему што радимо“, каже Генесеретх. Лекари запошљавају логику да дијагностицирају пацијенте, адвокати користе логичке аргументе у судници и логика је битнија него икад да се икада процени на брзо променљиву свет око нас, бележи. „То не има везе са математиком и формулама и алгебрима“, додаје Генесеретх.
О подржавању научног новинарства
Ако уживате у овом чланку, размислите о подршци нашем награђиваном новинарству Претплата. Куповином претплате помажете да се осигура будућност утицајних прича о открићима и идејама које данас у облику света у облику света.
Већина овогодишњих победника има интересовање за рачунарску науку, поред науке о животној средини, примењено математичко и електротехнику, али Зханг каже да ни математика ни рачунарска наука нису његово „снажно одијело“ и да планира да пређе у политичку науку. „Много проблема је потребно врло експанзивно размишљање и креативна решења и мислим да ће ми то дефинитивно помоћи ако у будућности улазим у политику“, објашњава он.
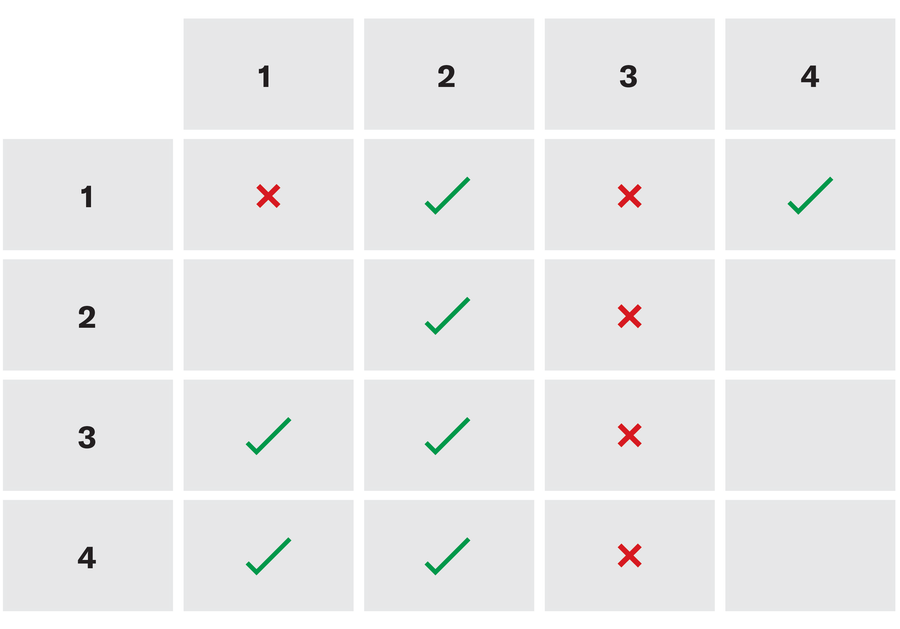
Посебан аспект олимпијаде је његова колаборативна природа, у којој тимови раде заједно да би решили проблеме, каже Иин. Посебно је био поносан како је он и његови саиграчи сарађивали на загонетку називе народи (доњи део). Након што је образложио да решење које је понудио један од чланова његове групе мора бити погрешан и смислио се алтернативним што је показало исправно, да сам се саиграч „управо наставио да ми каже колико је срећан да је имао да ме има срећу да ме је имао срећу да ме је имао у његовом тиму“ „Каже да је иин. „Имати ове невероватне људе да раде на логици – то је нешто што заједно уједињује нашу групу пријатеља.“
Ево неколико курираних загонетки из конкуренције које можете испробати руку са својом групом пријатеља. Неке од загонетки су измењене да би боље одговарали формату овог чланка.
Пријатељи
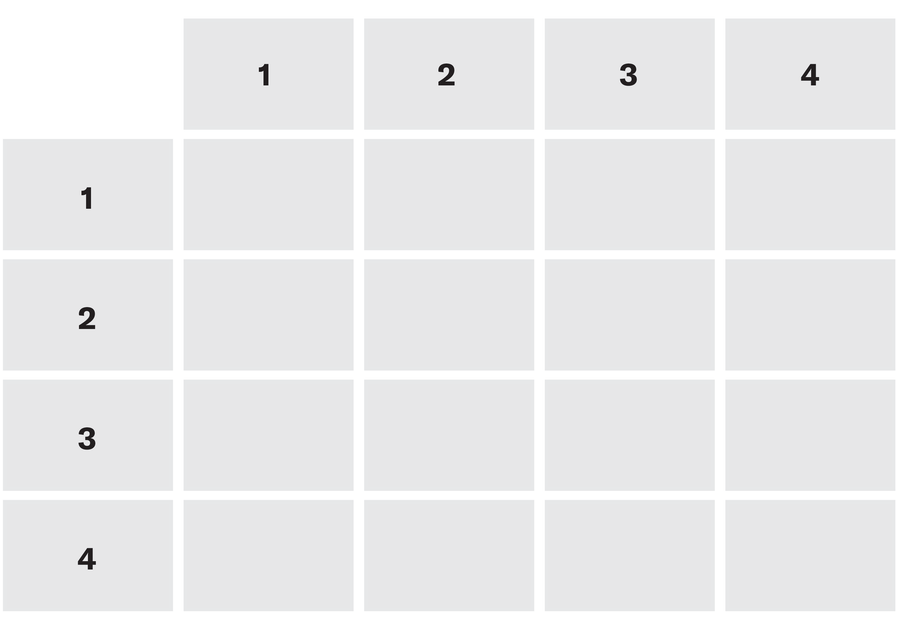
Четири студента, нумерисана 1, 2, 3 и 4, гласају међу собом да би утврдили ко би требало да води своју сесију прегледа. Сваки студент је дужан да гласа „да“ или „не“ за сваку особу у групи, укључујући себе. Следе истините изјаве о њиховим гласачким листићима:

У горњој табели, изјаве из оригиналног проблема ИЛО на језику математичке логике су у праву. Наши преводи тих изјава су са леве стране.
Одредите, у мери у којој је могуће из ових изјава, ко је то учинио и није гласао за кога. Испуните то у следећој мрежи са чеком да гласа, „Кс“ без гласа и празно ако не можете сигурно знати. Сваки ред представља гласачки листић броја наведеног са леве стране.
Напомена: Ако имамо изјаву А то није тачно, сматрамо било какву реченицу форме „ако А, онда Б„Бити истинит. На пример,“ Ако је небо зелено, онда је ____ „тачно без обзира на то што је празно јер је премиса лажна. Требат ће вам та чињеница да бисте је потребна загонетка.
Квиз
1. Који је одговор на питање 2?
А. Б
Б. А
Ц. Д
Д. Ц
2 Који је одговор на питање 3?
А. Ц
Б. Д
Ц. Б
Д. А
3. Који је одговор на питање 4?
А. Д
Б. А
Ц. Ц
Д. Б
4. Шта је одговор на питање 1?
А. Д
Б. Ц
Ц. А
Д. Б
Сигурно пуцање
Отворен је комбинација сефа са серијом од четири прекидача који се могу пребацити на (1) или искључено (0). Сеф је сломљен, па да бисте га отворили, само требате да стекнете положај два одређена прекидача тачне – али не постоји начин да знате који су прекидачи онима који су важни. Пронађите најмањи скуп комбинација које можете покушати да гарантујете да ће један од њих отворити сеф.
Нације
Постоје две врсте нација: снажна и слаба. Само слабе нације могу се напасти, а само јаке нације могу назвати. Ако снажна нација напади слабу нацију, анексираће слабим нацијом, али ће постати слаба и на тај начин је у неко време неко време. Само једна јака нација може у то време нападнути слабу нацију. Ако више нација одлуче да нападну исту слабу нацију, један је насумично изабран да би било дозвољено да се нападне. Свака нација жели да буде што је што већа што је могуће, али не и на штету да се приложи. Претпоставимо да су све нације потпуно рационалне. Постоји пет јаких нација и једна слаба нација. Да ли ће се слаба нација нападнути?
Савет: Покушајте почети са једном снажном нацијом и једном слабом нацијом, а затим се надоградите одатле. Да бисте решили проблем, покушајте да видите како се сложени случајеви могу смањити на једноставније и Нокиа; -а формално позната као „математичка индукција“.
Судоку слагалица
Ова слагалица је такође била укључена у ИЛО. Такмичари су га морали решити под временским границом користећи само оловку и папир.
Пријатељи
Квиз
1. Д
2 ц
3. б
4. а
Сигурно пуцање
Да бисте гарантовали да можете пукнути сеф, мораћете да имате сваки могући скуп позиција за сваки пар прекидача заступљених. На тај начин, без обзира које су два прекидача онима који су важни или који позиције отварају сеф, један од кодова ће га пробити. Минимални број потребних комбинација је пет. Ево једног могућег решења: 1000, 0100, 0010, 0001, 1111.
Нације
Ево једног начина да се то размислите. Претпоставимо да имамо једну снажну нацију и једну слабу нацију. Снажна нација природно ће желети да нападне слабицу, јер не постоји други народ да напада снажног након што то учини. Шта је са две јаке нације и једна слаба нација? Па, ако је једна од снажних нација била да се примери слаби нацији, привремено би постала слаба и да га је друга напада, тако да ни једно од њих не би желео да на првом месту не би нападнули, знајући да ће се вратити одмах назад. Сада размотрите три јаке нације и једну слабу нацију: поново, ако се снажна нација упада, остало нам је са две снажне нације и једну слабу нацију, ситуацију у којој само нисмо утврдили да нико не би у овом случају желели да у овом случају не би желели да нападну у овом случају, остали смо снажне нације. Користећи исту логику, ако постоје четири снажне нације, а један напада, сценариј ће се смањити на случај тро-снажних нација где би сви желели да нападну, тако да ниједна од четири нације не би ризиковала на прво место. Коначно, то нас води до пет јаких нација и једне слабе нације, сценариј у којем би све јаке нације желеле да нападну јер, након што постоје четири јаке нације и оне које је постало слаб од анекса, нико неће назвати.