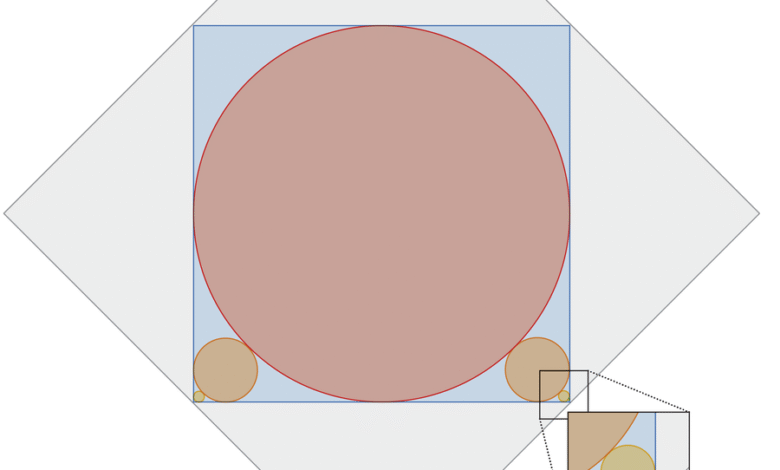
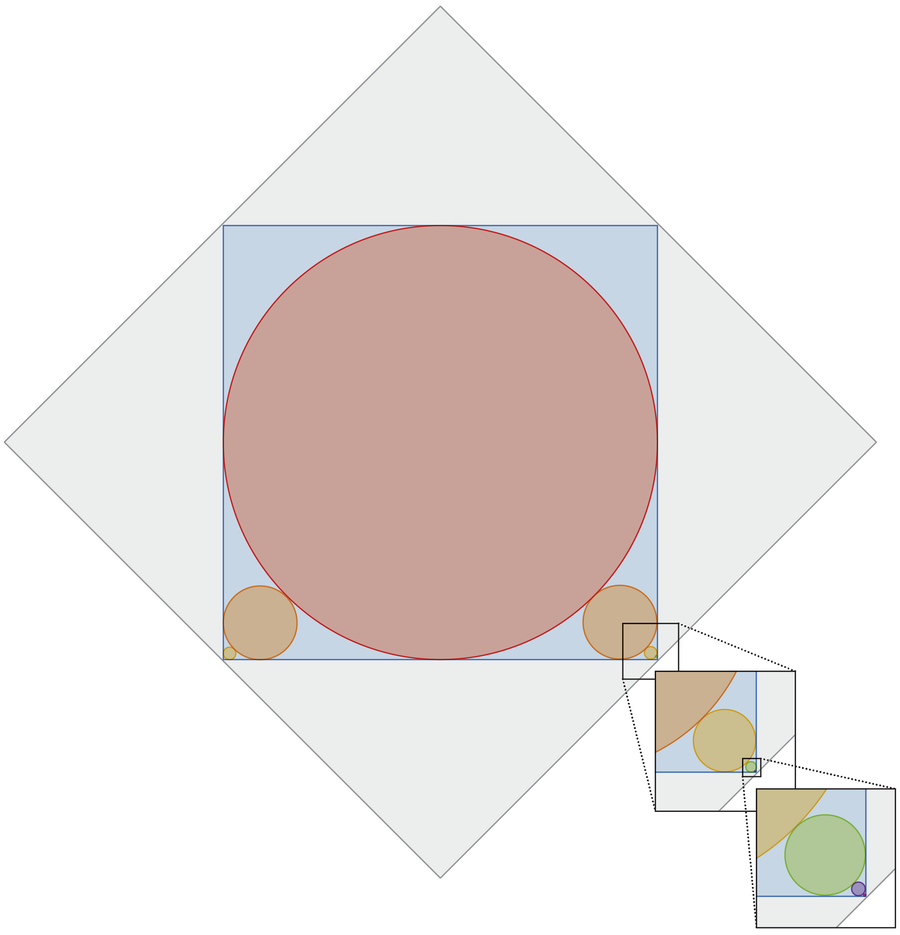
Црвени круг је уписан у плави квадрат. Аранжман оставља празнине у четири угла квадрата, од којих су два испуњена мањим круговима који једва додирују велики црвени круг и две угаоне стране плавог квадрата. Ово, пак, оставља две мање празнине у угловима, који су испуњени мањим круговима, и тако даље, све мањим круговима до бесконачности. Цео дијаграм је уписан унутар сивог квадрата 1 × 1. Колики је укупан обим свих кругова?
Укупан обим свих кругова је π. Обим круга је π пута већи од његовог пречника. Дакле, укупан обим многих кругова са пречницима д1, д2, д3,… је:
πд1 + πд2 + πд3 + … = π(д1 + д2 + д3 + …)
Дакле, ако можемо да пронађемо збир свих пречника, можемо ту вредност помножити са π и готови смо. Због симетрије, величине кругова се не мењају ако неке померимо у различите углове:
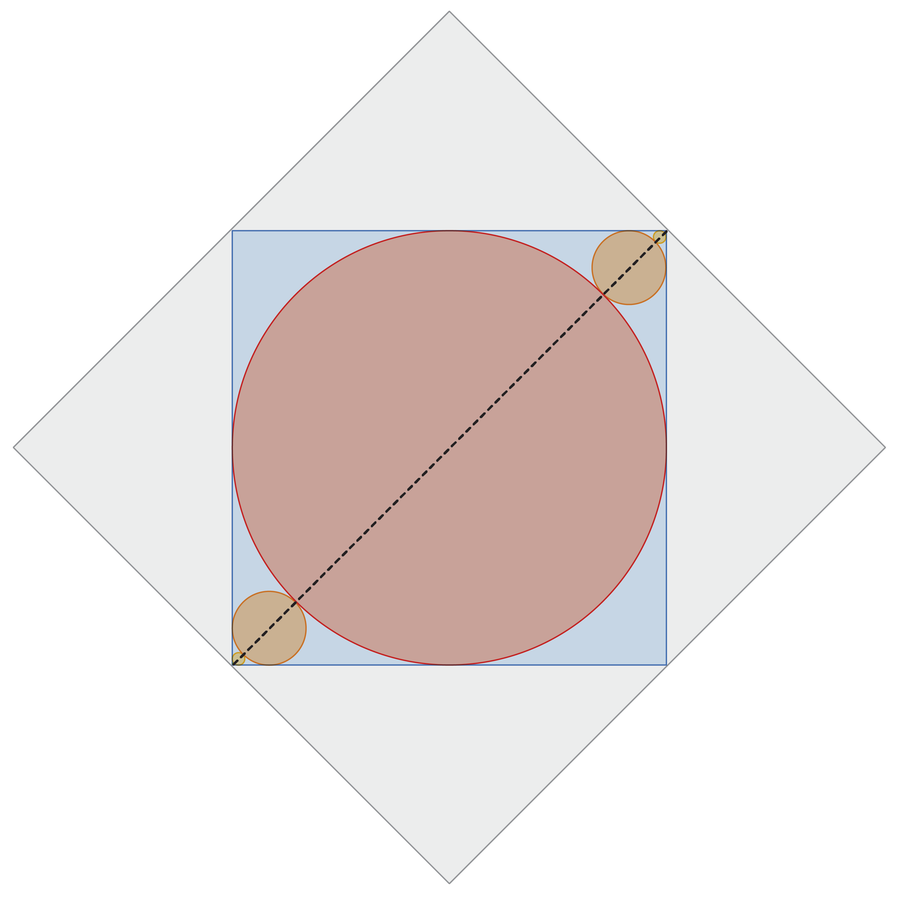
Пошто бесконачно много кругова тежи ка угловима плавог квадрата, збир пречника кругова једнак је дужини дијагонале плавог квадрата (приказан као испрекидана линија). Ова дужина је једнака 1 јер спољни сиви квадрат има дужину странице 1.
Волели бисмо да чујемо од вас! Пошаљите нам е-пошту на гамес@сциам.цом да поделите своје искуство.